3.4 KiB
# Homotopy Levels
The loop space can contain higher homotopical information that
the fundamental group does not capture.
For example, consider S².
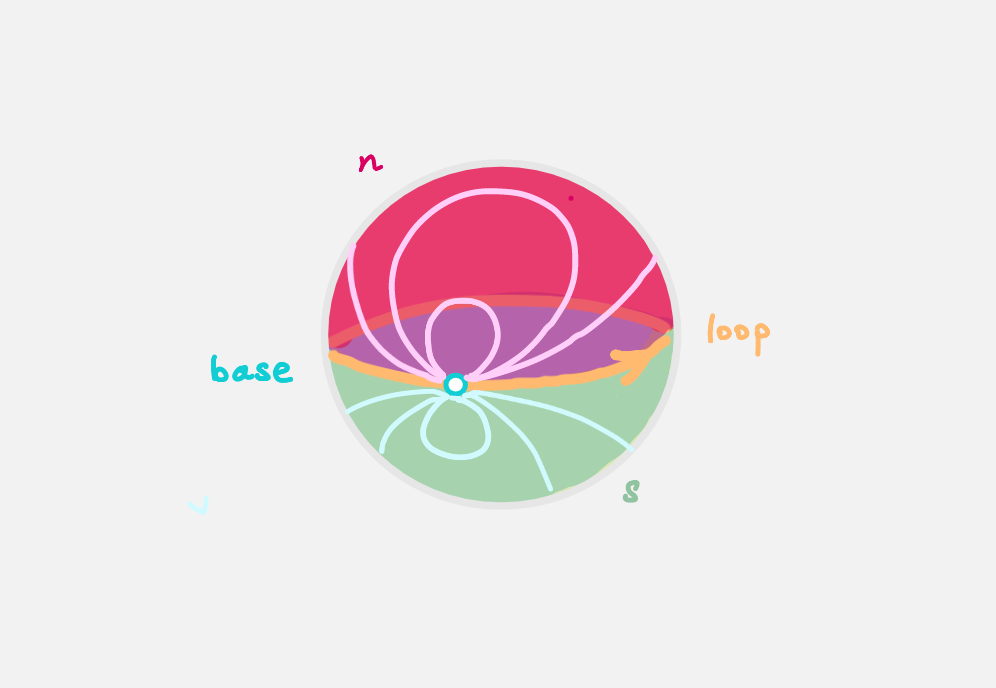
data S² : Type where
base : S²
loop : base ≡ base
northHemisphere : loop ≡ refl
southHemisphere : refl ≡ loop
What is `refl`?
For any space A and point a : A,
refl is the constant path at a.
Technically speaking, we should write refl a to indicate the point we are at,
however agda is often smart enough to figure that out.
Intuitively, all loops in S² based at base is homotopic to
the constant path refl.
In other words, the fundamental group at base of S² is trivial.
However, the 'composition' of the path southHemisphere with northHemisphere
in base ≡ base gives the surface of S²,
which intuitively is not homotopic to the constant point base.
So base ≡ base has non-trivial path structure.
Let's be more precise about homotopical data :
We can check that a space is 'homotopically trivial' (h-trivial)
from dimension n
by checking if spheres of dimension n can be filled.
To be h-trivial from 0 is for any two points
to have a line in between; to fill S⁰.
This data is captured in
isProp : Type → Type
isProp A = (x y : A) → x ≡ y
All maps are continuous in HoTT
There is a subtlety in the definition isProp.
This is stronger than saying that the space A is path connected.
Since A is equipped with a continuous map taking pairs x y : A
to a path between them.
We will show that isProp S¹ is empty despite S¹ being path connected.
Similarly, to be h-trivial from dimension 1 is for any two points x y : A
and any two paths p q : x ≡ y to have a homotopy from p to q;
to fill S¹. This is captured in
isSet : Type → Type
isSet A = (x y : A) → isProp (x ≡ y)
To define the fundamental group we will make the loop space satisfy
isSet by trucating the loop space'.
First we show that isProp S¹ and isSet S¹ are both empty.
Locate ¬isSetS¹ in 1FundamentalGroup/Quest1.agda.
In the cubical library we have the result
isProp→isSet : (A : Type) → isProp A → isSet A
which we will not prove.
Assuming ¬isSetS¹, use isProp→isSet to deduce ¬isPropS¹.
HLevel
Generalisation to HLevel and isHLevel n → isHLevel suc n??
Turning our attention to ¬isSetS¹,
again given h : isSet S¹ -
a map continuously taking each pair x y : A
to a point in isProp (x ≡ y).
We can apply h twice to the only point base available to us,
obtaining a point of isProp (base ≡ base).
Try mapping from this into the empty space.
Hint 0
We have already shown that Refl ≡ loop is the empty space.
We have imported Quest0Solutions.agda for you,
so you can just quote the result from there.
Hint 1
- assume
h - type
Refl≢loopit in the hole and refine - it should now be asking for a proof that
Refl ≡ loop - try to use
h