`Refl ≡ loop` is empty

To get a better feel of S¹, we show that the space of paths (homotopies) between Refl and loop, written Refl ≡ loop, is empty. First, we define the empty space and what it means for a space to be empty. Here is what this looks like in agda :

data ⊥ : Type where

This says "the empty space ⊥ is a space with no points in it".

Here are three candidate definitions for a space A to be empty :

there is a point f : A → ⊥ in the space of functions from A to the empty space
there is a path p : A ≡ ⊥ in the space of spaces Type from A to the empty space
there is an isomorphism i : A ≅ ⊥ of spaces

These turn out to be 'the same' (see 1FundamentalGroup/Quest0SideQuests/SideQuest0), however for our present purposes we will use the first definition. Our goal is therefore to produce a point in the function space

( Refl ≡ loop ) → ⊥

The authors of this series have thought long and hard about how one would come up with the following argument. Unfortunately, sometimes mathematics is in need of a new trick and this was one of them.

The trick is to make a path p : true ≡ false from the assumed path (homotopy) h : Refl ≡ loop by constructing a non-trivial Bool-bundle over the circle, hence obtaining a map ( Refl ≡ loop ) → ⊥.

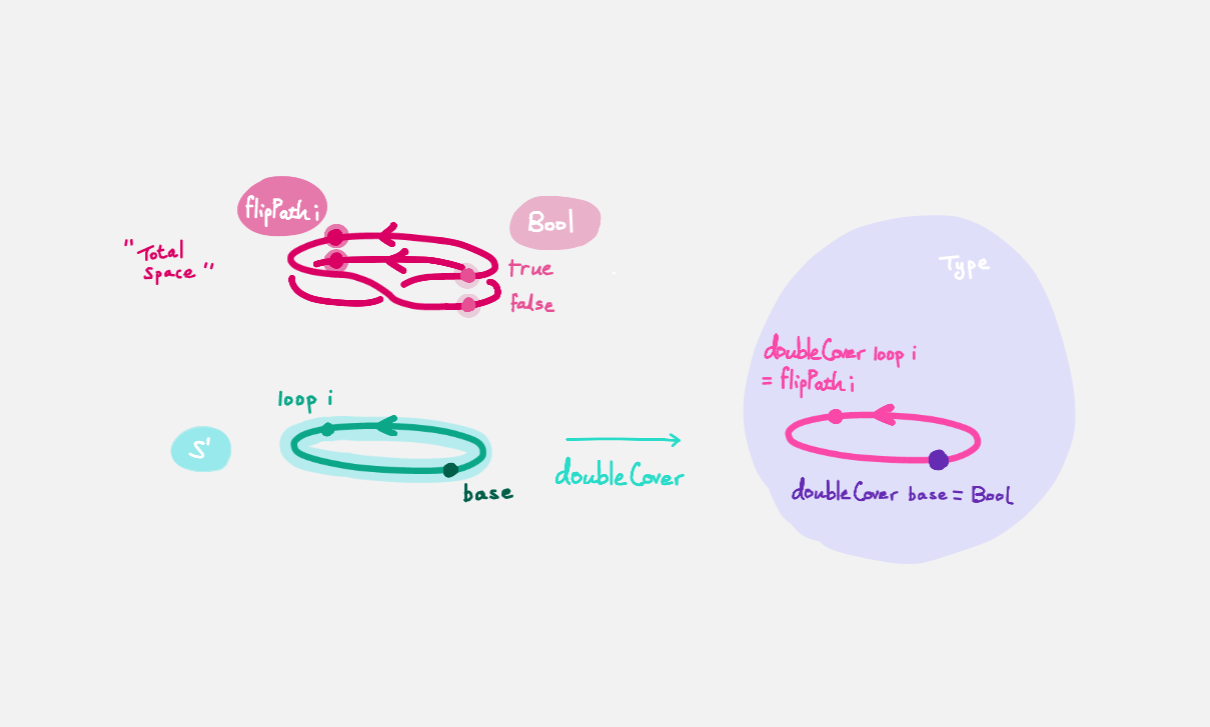
To elaborate : Bool here refers to the discrete space with two points true, false. (To find out the definition of Bool in agda you can hover over Bool in agda and use M-SPC c d.) We will create a map doubleCover : S¹ → Type that sends base to Bool and the path loop to a non-trivial path flipPath : Bool ≡ Bool in the space of spaces.

Viewing the picture vertically, for each point x : S¹, we call doubleCover x the fiber of doubleCover over x. All the fibers look like Bool, hence our choice of the name Bool-bundle.

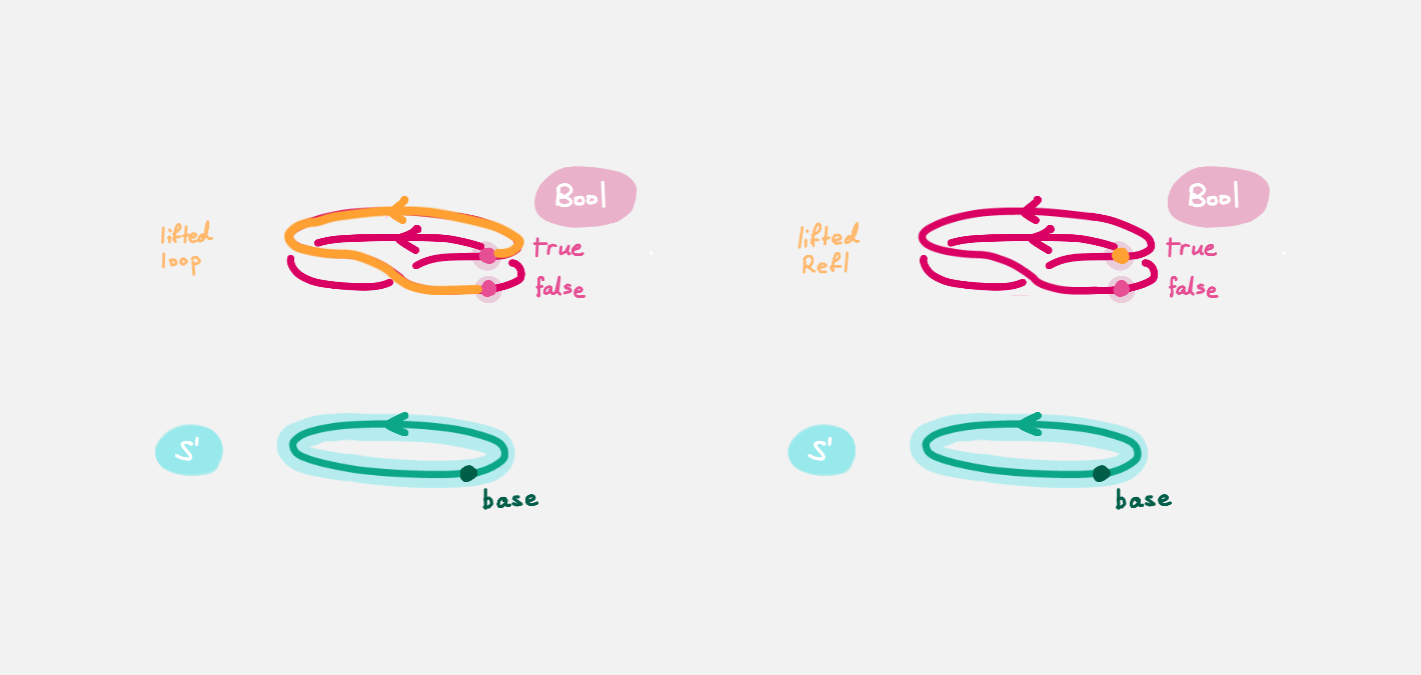
We will get a path from true to false in the fiber of doubleCover over base by 'lifting the homotopy' h : Refl ≡ loop and considering the end points of the 'lifted paths'. Refl will 'lift' to a 'constant path' and loop will 'lift' to

Let's assume for the moment that we have flipPath already and define doubleCover.

Navigate to the definition of doubleCover and make sure you have loaded the file with C-c C-l.
```
doubleCover : S¹ → Type
doubleCover x = {!!}
```
Navigate your cursor to the hole, write x and do C-c C-c. The c stands for cases. You should now see two new holes :
```
doubleCover : S¹ → Type
doubleCover base = {!!}
doubleCover (loop i) = {!!} 
```
This means : S¹ is made from a point base and an edge loop, so a map out of S¹ to a space is the same as choosing a point and an edge to map base and loop to respectively. Since loop is a path from base to itself, its image must also be a path from the image of base to itself.
Use C-c C-f and/or C-c C-b to navigate to the first hole. We want to map base to Bool so fill the hole with Bool using C-c C-SPC.
Navigate to the second hole. Here loop i is a generic point in the path loop, where i : I is a generic point of the 'unit interval'. We want to map loop to flipPath, so loop i should map to a generic point in the path flipPath. Try filling the hole.
Once you think you are done, reload the agda file with C-c C-l and if it doesn't complain this means there are no problems with your definition.

Defining flipPath is quite involved and we will do so in the next quest!

3.8 KiB Raw Blame History

Refl ≡ loop is empty

3.8 KiB

Raw Blame History

`Refl ≡ loop` is empty