TheHoTTGame/Trinitarianism/Quest0.md

There are three ways of looking at A : Type u.

• proof theoretically, 'A is a proposition'
• type theoretically, 'A is a construction'
• categorically, 'A is an object in category Type u'

We will explain what u : Level and Type u is at the end.

A first example of a type construction is the function type. Given types A and B, we have another type A → B which can be seen as

• the proposition 'A implies B'
• the construction 'ways to convert A recipes to B recipes'
• internal hom of the category Type u

To give examples of this, let's make some types first!

-- Here is how we define 'true'
data ⊤ : Type u where
  trivial : ⊤

It reads '⊤ is an inductive type with a constructor trivial', with three interpretations

• ⊤ is a proposition and there is a proof of it, called trivial.
• ⊤ is a construction with a recipe called trivial
• ⊤ is a terminal object: every object has a morphism into ⊤ given by · ↦ trivial

The above tells you how we make a term of type ⊤, let's see an example of using a term of type ⊤:

TrueToTrue : ⊤ → ⊤
TrueToTrue = {!!}

• press C-c C-l (this means Ctrl-c Ctrl-l) to load the document, and now you can fill the holes
• navigate to the hole { } using C-c C-f (forward) or C-c C-b (backward)
• press C-c C-r and agda will try to help you (r for refine)
• you should see λ x → { }
• navigate to the new hole
• C-c C-, to check the goal (C-c C-comma)
• the Goal area should look like

Goal: ⊤
—————————————————————————
x : ⊤

• you have a proof/recipe/generalized element x : ⊤ and you need to give a p/r/g.e. of ⊤
• you can give it a p/r/g.e. of ⊤ and press C-c C-SPC to fill the hole

There is more than one proof (see solutions) - are they the same? Here is an important one:

TrueToTrue' : ⊤ → ⊤
TrueToTrue' x = {!!}

• Naviagate to the hole and check the goal.
• Note x is already taken out for you.
• You can try type x in the hole and C-c C-c
• c stands for 'cases on x' and the only case is trivial.

Built into the definition of ⊤ is agda's way of making a map out of ⊤ into another type A, which we have just used. It says to map out of ⊤ it suffices to do the case when x is trivial, or

• the only proof of ⊤ is trivial
• the only recipe for ⊤ is trivial
• the only one generalized element trivial in ⊤

-- Here is how we define 'false'
data ⊥ : Type u where

It reads '⊥ is an inductive type with no constructors', with three interepretations

• ⊥ is a proposition with no proofs
• ⊥ is a construction with no recipes
• There are no generalized elements of ⊥ (it is a strict initial object)

Let's try mapping out of ⊥.

explosion : ⊥ → ⊤
explosion x = {!!}

• Navigate to the hole and do cases on x.

Agda knows that there are no cases so there is nothing to do! This has three interpretations:

• false implies anything (principle of explosion)
• ?
• ⊥ is initial in the category Type u

We can also encode "natural numbers" as a type.

data ℕ : Type where
  zero : ℕ
  suc : ℕ → ℕ

As a construction, this reads '

• ℕ is a type of construction
• zero is a recipe for ℕ
• suc takes an existing recipe for ℕ and gives another recipe for ℕ. '

We can see ℕ as a categorical notion: ℕ is a natural numbers object in the category Type u, with zero : ⊤ → ℕ and suc : ℕ → ℕ such that given any ⊤ → A → A there exist a unique morphism ℕ → A such that the diagram commutes:

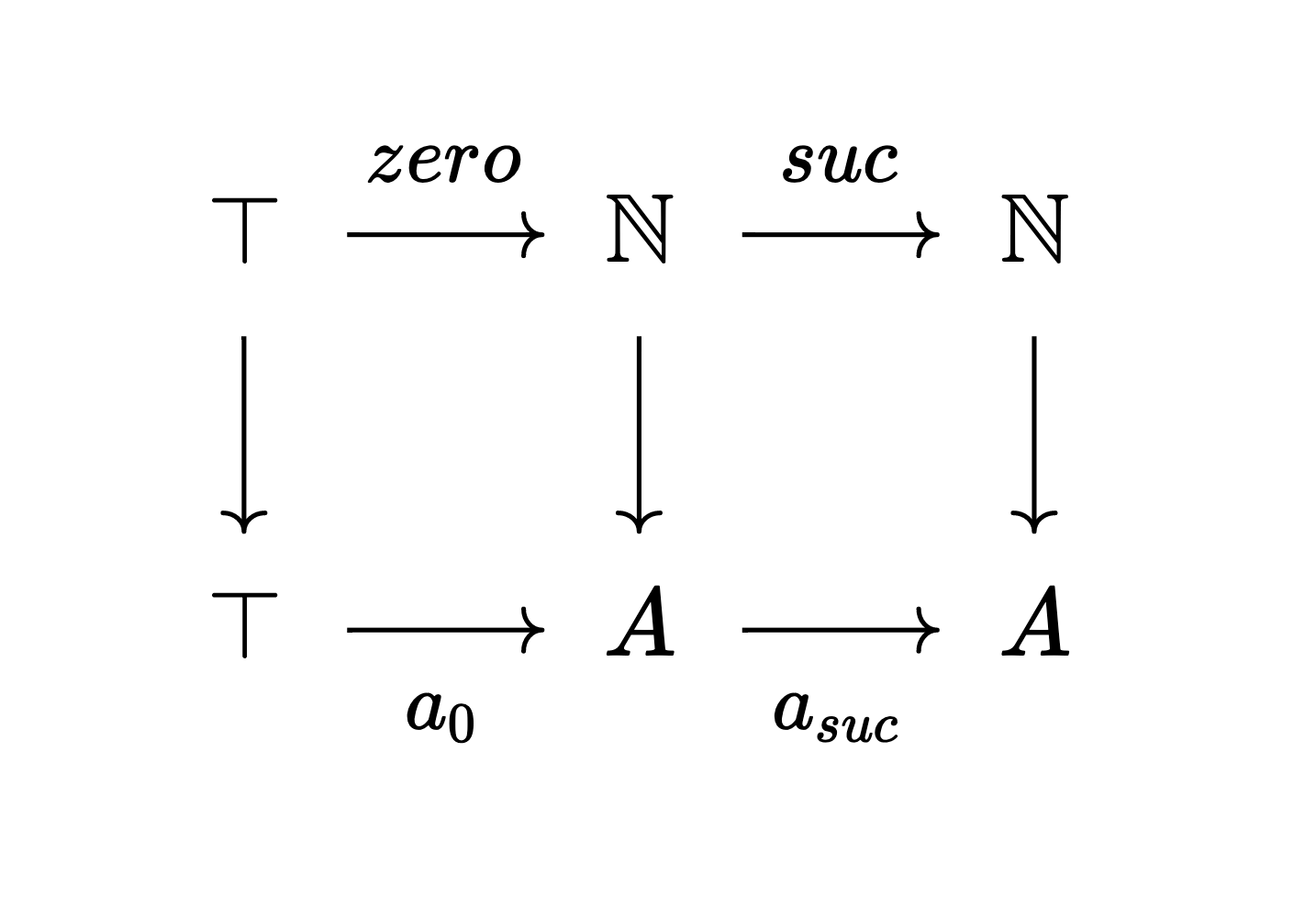
This has no interpretation as a proposition since there are too many terms, since mathematicians classically didn't distinguish between proofs of the same thing. (ZFC doesn't even mention logic internally, unlike Type Theory!)

-}