Dependent Types and Sigma Types

In a 'place to do maths' we would like to be able to express and 'prove' the statement

There exists a natural that is even.

This requires the notion of a predicate. In general a predicate on a type A : Type is a term of type A → Type. For example,

isEven : ℕ → Type
isEven n = ?

Do C-c C-l to load the file.
Navigate to the hole.
Input n in the hole and do C-c C-c. You should now see
```
isEven : ℕ → Type
isEven zero = {!!}
isEven (suc n) = {!!}
```
It says "to define a function on ℕ, it suffices to define the function on the cases, zero and suc n, since these are the only constructors given in the definition of ℕ." This has the following interpretations :
- propositionally, this is the principle of mathematical induction.
- categorically, this is the universal property of a natural numbers object.
Navigate to the first hole and check the goal. You should see
```
Goal: Type
———————————
```
Fill the hole with ⊤, since we want zero to be even.
Navigate to the second hole.

Input n and do C-c C-c again. You should now see

isEven : ℕ → Type
isEven zero = ⊤
isEven (suc zero) = {!!}
isEven (suc (suc n)) = {!!}

We have just used induction again.

Navigate to the first hole and check the goal. Agda should be asking for a term of type Type, so fill the hole with ⊥, since we don't want suc zero to be even.
Navigate to the next hole and check the goal. You should see in the 'agda information' window,
```
Goal: Type
——————————————
n : ℕ
```
We are in the 'inductive step', so we have access to the previous natural number.
Fill the hole with isEven n, since we want suc (suc n) to be even precisely when n is even.

The reason we have access to the term isEven n is again because we are in the 'inductive step'.
There should now be nothing in the 'agda info' window. This means everything is working.

There are three interpretations of isEven : ℕ → Type.

Already mentioned, isEven is a predicate on ℕ.
isEven is a dependent construction. Specifically, isEven n is either ⊤ or ⊥ depending on n : ℕ.
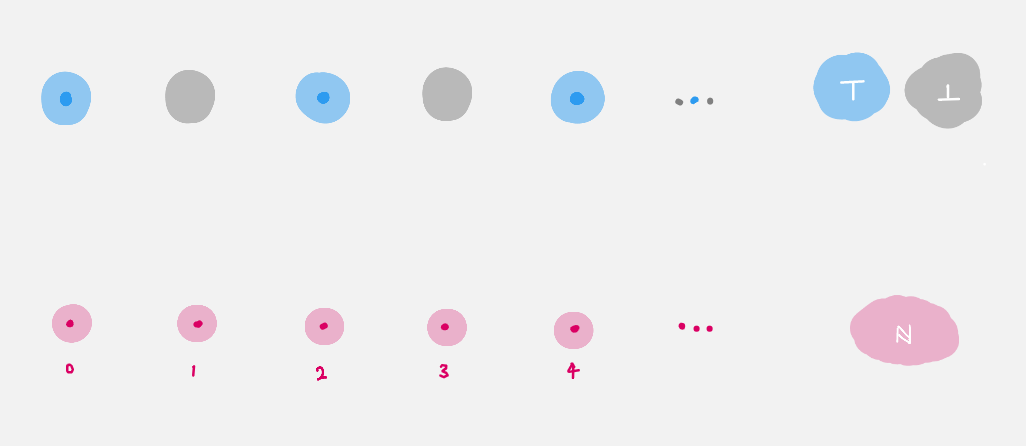
isEven is a bundle over ℕ, i.e. an object in the over-category Type↓ℕ. Pictorially, it looks like

In the categorical perspective, for each n : ℕ isEven n is called the fiber over n. In this particular example the fibers are either empty or singleton.

In general given a type A : Type, a dependent type over A is a term of type A → Type.

You can check if 2 is even by asking agda to 'reduce' the term isEven 2: do C-c C-n (n for normalize) and type in isEven 2. (By the way you can write in numerals since we are now secretly using ℕ from the cubical agda library.)

Now that we have expressed isEven we need to be able write down "existence". In maths we might write

∃ x ∈ ℕ, isEven x

which in agda notation is

Σ ℕ isEven

This is called a sigma type, which has three interpretations:

the proposition 'there exists an even natural'
the construction 'keep a recipe n of naturals together with a recipe of isEven n'
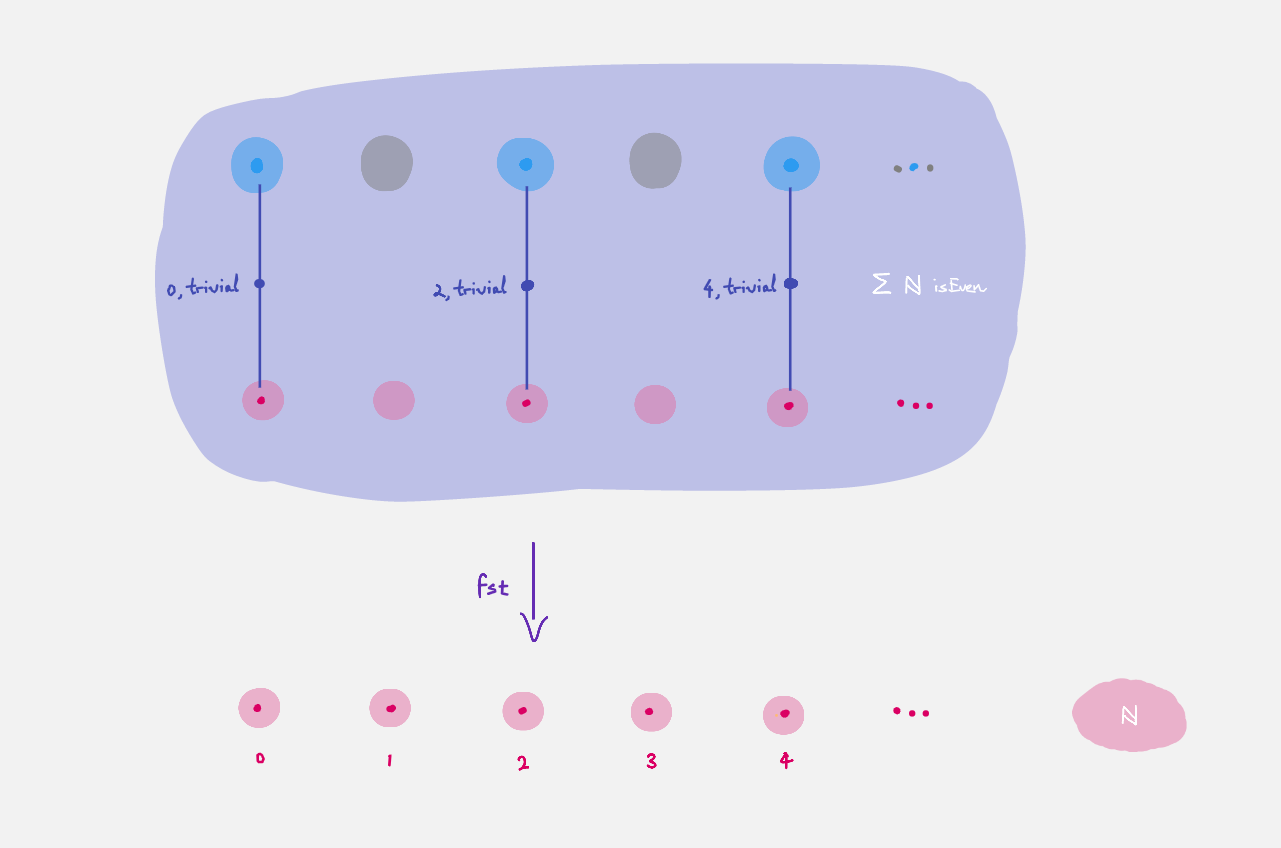
the total space of the bundle isEven over ℕ, which is the space obtained by putting together all the fibers. Pictorially, it looks like

which can also be viewed as the subset of even naturals, since the fibers are either empty or singleton. (It is a subsingleton bundle).

Making a term of this type has three interpretations:

a natural n : ℕ together with a proof hn : isEven n that n is even.
a recipe n : ℕ together with a recipe hn : isEven n.
a point in the total space is a point n : ℕ downstairs together with a point hn : isEven n in its fiber.

Now you can prove that there exists an even natural:

Formulate the statement you need. Make sure you have it of the form

Name : Statement
Name = ?

Load the file, go to the hole and refine the goal.
If you formulated the statement right it should split into {!!} , {!!} and you can check the types of terms the holes require.
Fill the holes. There are many proofs you can do!

In general when A : Type is a type and B : A → Type is a predicate/dependent construction/bundle over A, we can write the sigma type Σ A B whose terms are pairs a , b where a : A and b : B a. In the special case when B is not dependent on a : A, i.e. it looks like λ a → C for some C : Type then Σ A B is just

the proposition 'A and C' since giving a proof of this is the same as giving a proof of A and a proof of C
a recipe a : A together with a recipe c : C
B is now a trivial bundle since the fibers B a are constant with respect to a : A. In other words it is just a product Σ A B ≅ A × C. For this reason, some refer to the sigma type as the dependent product, but we will avoid this terminology.

_×_ : Type → Type → Type
A × C = Σ A (λ a → C)

Agda supports the notation _×_ (without spaces) which means from now on you can write A × C (with spaces).

There are two ways of using a term in a sigma type. We can extract the first part using fst or the second part using snd. Given x : Σ A B there are three interpretations of fst and snd:

Viewing x as a proof of existence fst x provides the witness of existence and snd provides the proof that the witness fst x has the desired property
Viewing x as a recipe fst extracts the first component and snd extracts the second component
Viewing x as a point in the total space of a bundle fst x is the point that x is over in the base space and snd x is the point in the fiber that x represents. In particular you can interpret fst as projection from the total space to the base space, collapsing fibers. For example to define a map that takes an even natural and divides it by two we can do

div2 : Σ ℕ isEven → ℕ
div2 x = ?

Load the file, go to the hole and case on x. You might want to rename fst₁ and snd₁.
```
div2 : Σ ℕ isEven → ℕ
div2 (fst₁ , snd₁) = {!!}
```

Case on fst₁ and tell agda what to give for 0 , _, i.e. what 'zero divided by two' ought to be.

div2 : Σ ℕ isEven → ℕ
div2 (zero , snd₁) = {!!}
div2 (suc fst₁ , snd₁) = {!!}

Navigate to the second hole and case on fst₁ again. Notice that agda knows there is no term looking like 1 , _ so it has skipped that case for us.
```
div2 : Σ ℕ isEven → ℕ
div2 (zero , snd₁) = 0
div2 (suc (suc fst₁) , snd₁) = {!!}
```
(n + 2) / 2 should just be n/2 + 1 so try writing in suc and refining the goal
How do you write down n/2? Hint: we are in the 'inductive step'.

Try dividing some terms by 2:

Use C-c C-n and write div2 (2 , tt) for example.
Try dividing 36 by 2.

Important Observation : the two proofs 2 , tt and 36 , tt of the statement 'there exists an even natural' are not 'the same' in any sense, since if they were div2 (2 , tt) would be 'the same' div2 (36/2 , tt), and hence 1 would be 'the same' as 18.

Are they 'the same'? What is 'the same'?

7.6 KiB Raw Blame History Unescape Escape

Dependent Types and Sigma Types

7.6 KiB

Raw Blame History