| .. | ||
| bin | ||
| images | ||
| Preambles | ||
| .DS_Store | ||
| Quest0.agda | ||
| Quest0.md | ||
| Quest0Solutions.agda | ||
| Quest1.agda | ||
| Quest1.md | ||
| Quest1Solutions.agda | ||
| Quest2.agda | ||
| Quest2.md | ||
| Quest2Solutions.agda | ||
| README.md | ||
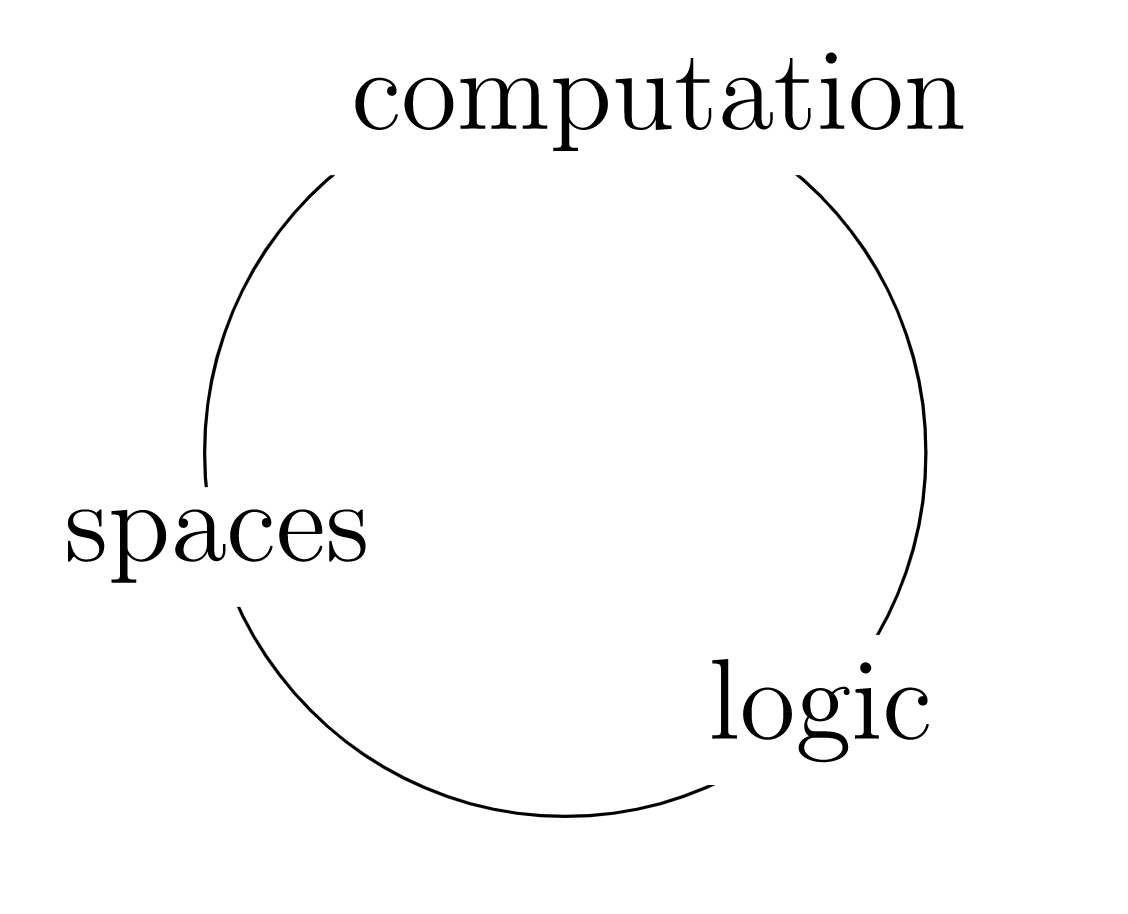
Trinitarianism
By the end of this arc we will (almost) have 'a place to do maths'. The 'types' that will populated this 'place' will have three interpretations:
- Proof theoretically, with types as propositions
- Type theoretically, with types as programs
- Category theoretically, with types as objects in a category
Terms and Types
Here are some things that we could like to have in a 'place to do maths'
- objects to reason about (E.g.
ℕ) - recipes for making things inside objects
(E.g.
n + mfornandmin naturals.) - propositions to reason with (E.g.
n = 0fornin naturals.)
In proof theory, types are propositions and terms of a type are their proofs. In type theory, types are programs / constructions and terms are algorithms / recipes. In category theory, types are objects and terms are generalised elements.
Non-dependent Types
- false / empty / initial object
- true / unit / terminal object
- or / sum / coproduct
- and / pairs / product
- implication / functions / internal hom
Dependent Types
- predicate / type family / bundle
- substitution / substitution / pullback (of bundles)
- existence / Σ type / total space of bundles
- for all / Π type / space of sections of bundles
Something doesn't feel the Same
There will be one thing missing from this 'place to do maths' and that is a notion of equality. This is where HoTT deviates from its predecessors, and is the theme of the next arc.