# Dependent Types and Sigma Types
In a 'place to do maths'
we would like to be able to express and 'prove'
the statement
> There exists a natural that is even.
This requires the notion of a _predicate_.
In general a predicate on a type `A : Type` is
a term of type `A → Type`.
For example,
```agda
isEven : ℕ → Type
isEven n = ?
```
- Do `C-c C-l` to load the file.
- Navigate to the hole.
- Input `n` in the hole and do `C-c C-c`.
You should now see
```agda
isEven : ℕ → Type
isEven zero = {!!}
isEven (suc n) = {!!}
```
It says "to define a function on `ℕ`,
it suffices to define the function on the _cases_,
`zero` and `suc n`,
since these are the only constructors given
in the definition of `ℕ`."
This has the following interpretations :
- propositionally, this is the _principle of mathematical induction_.
- categorically, this is the universal property of a
natural numbers object.
- Navigate to the first hole and check the goal.
You should see
```
Goal: Type
———————————
```
Fill the hole with `⊤`, since we want `zero` to be even.
- Navigate to the second hole.
- Input `n` and do `C-c C-c` again.
You should now see
```agda
isEven : ℕ → Type
isEven zero = ⊤
isEven (suc zero) = {!!}
isEven (suc (suc n)) = {!!}
```
We have just used induction again.
- Navigate to the first hole and check the goal.
Agda should be asking for a term of type `Type`,
so fill the hole with `⊥`,
since we don't want `suc zero` to be even.
- Navigate to the next hole and check the goal.
You should see in the 'agda information' window,
```
Goal: Type
——————————————
n : ℕ
```
We are in the 'inductive step',
so we have access to the previous natural number.
- Fill the hole with `isEven n`,
since we want `suc (suc n)` to be even _precisely when_
`n` is even.
The reason we have access to the term `isEven n` is again
because we are in the 'inductive step'.
- There should now be nothing in the 'agda info' window.
This means everything is working.
There are three interpretations of `isEven : ℕ → Type`.
- Already mentioned, `isEven` is a predicate on `ℕ`.
- `isEven` is a _dependent construction_.
Specifically, `isEven n` is either `⊤` or `⊥` depending on `n : ℕ`.
- `isEven` is a _bundle over `ℕ`_,
i.e. an object in the over-category `Type↓ℕ`.
Pictorially, it looks like
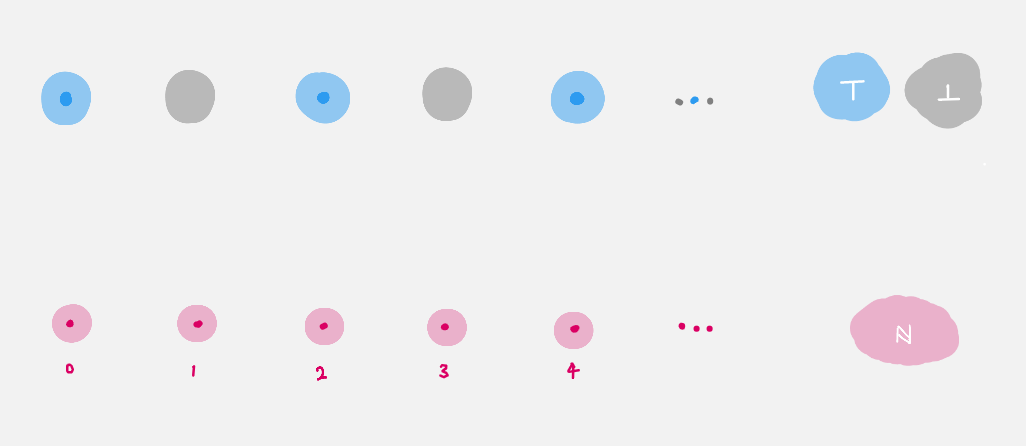 In the categorical perspective, for each `n : ℕ`
`isEven n` is called the _fiber over `n`_.
In this particular example the fibers are either empty
or singleton.
In general given a type `A : Type`,
a _dependent type over `A`_ is a term of type `A → Type`.
You can check if `2` is even by asking agda to 'reduce' the term `isEven 2`:
do `C-c C-n` (`n` for normalize) and type in `isEven 2`.
(By the way you can write in numerals since we are now secretly
using `ℕ` from the cubical agda library.)
Now that we have expressed `isEven` we need to be able write down "existence".
In maths we might write
```
∃ x ∈ ℕ, isEven x
```
which in agda notation is
```
Σ ℕ isEven
```
This is called a _sigma type_, which has three interpretations:
- the proposition 'there exists an even natural'
- the construction
'keep a recipe `n` of naturals together with a recipe of `isEven n`'
- the total space of the bundle `isEven` over `ℕ`,
which is the space obtained by putting together all the fibers.
Pictorially, it looks like
In the categorical perspective, for each `n : ℕ`
`isEven n` is called the _fiber over `n`_.
In this particular example the fibers are either empty
or singleton.
In general given a type `A : Type`,
a _dependent type over `A`_ is a term of type `A → Type`.
You can check if `2` is even by asking agda to 'reduce' the term `isEven 2`:
do `C-c C-n` (`n` for normalize) and type in `isEven 2`.
(By the way you can write in numerals since we are now secretly
using `ℕ` from the cubical agda library.)
Now that we have expressed `isEven` we need to be able write down "existence".
In maths we might write
```
∃ x ∈ ℕ, isEven x
```
which in agda notation is
```
Σ ℕ isEven
```
This is called a _sigma type_, which has three interpretations:
- the proposition 'there exists an even natural'
- the construction
'keep a recipe `n` of naturals together with a recipe of `isEven n`'
- the total space of the bundle `isEven` over `ℕ`,
which is the space obtained by putting together all the fibers.
Pictorially, it looks like
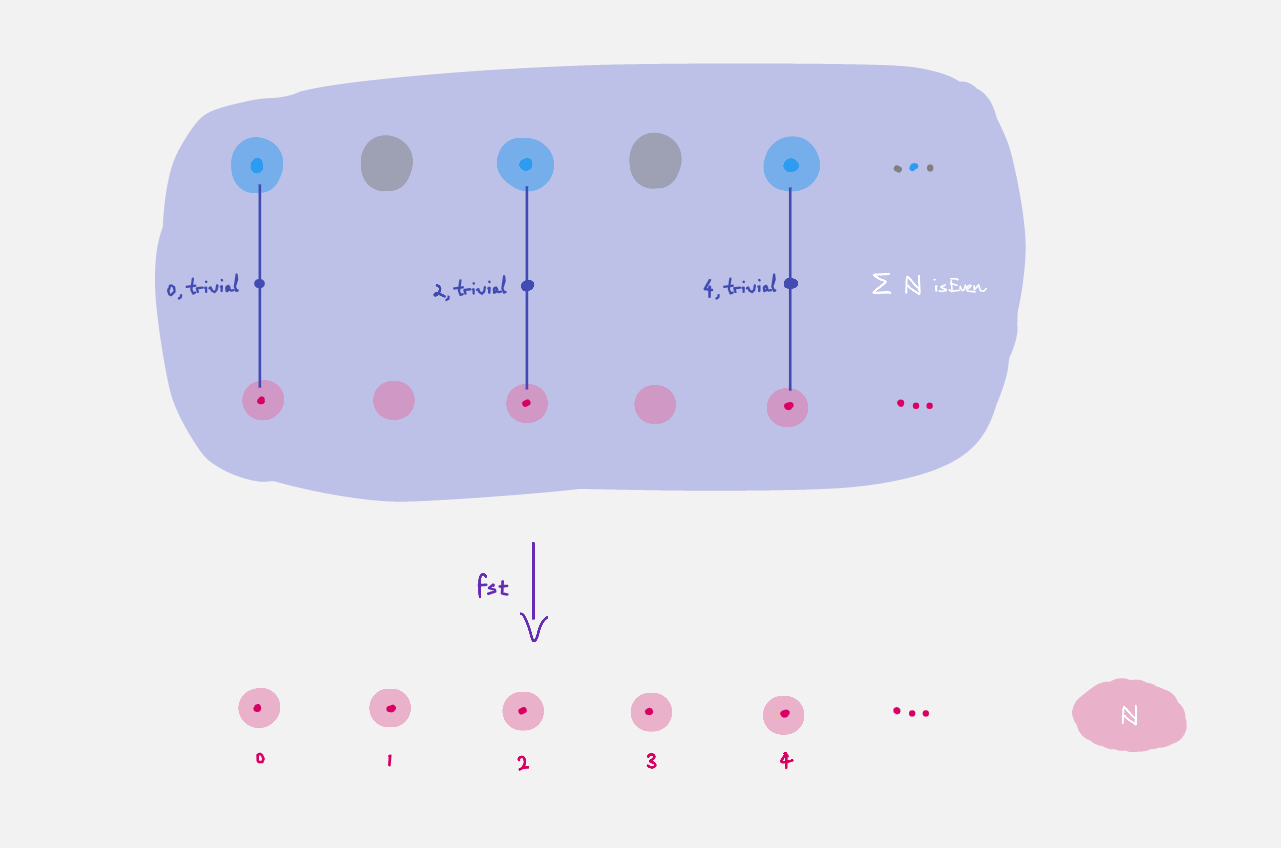 which can also be viewed as the subset of even naturals,
since the fibers are either empty or singleton.
(It is a _subsingleton bundle_).
Making a term of this type has three interpretations:
- a natural `n : ℕ` together with a proof `hn : isEven n` that `n` is even.
- a recipe `n : ℕ` together with a recipe `hn : isEven n`.
- a point in the total space is a point `n : ℕ` downstairs
together with a point `hn : isEven n` in its fiber.
Now you can prove that there exists an even natural:
- Formulate the statement you need. Make sure you have it of the form
```agda
Name : Statement
Name = ?
```
- Load the file, go to the hole and refine the goal.
- If you formulated the statement right it should split into `{!!} , {!!}`
and you can check the types of terms the holes require.
- Fill the holes. There are many proofs you can do!
In general when `A : Type` is a type and `B : A → Type` is a
predicate/dependent construction/bundle over `A`,
we can write the sigma type `Σ A B` whose terms are pairs `a , b`
where `a : A` and `b : B a`.
In the special case when `B` is not dependent on `a : A`,
i.e. it looks like `λ a → C` for some `C : Type` then
`Σ A B` is just
- the proposition '`A` and `C`'
since giving a proof of this is the same as giving a proof
of `A` and a proof of `C`
- a recipe `a : A` together with a recipe `c : C`
- `B` is now a _trivial bundle_ since the fibers `B a` are
constant with respect to `a : A`.
In other words it is just a _product_ `Σ A B ≅ A × C`.
For this reason,
some refer to the sigma type as the _dependent product_,
but we will avoid this terminology.
```agda
_×_ : Type → Type → Type
A × C = Σ A (λ a → C)
```
Agda supports the notation `_×_` (without spaces)
which means from now on you can write `A × C` (with spaces).
There are two ways of using a term in a sigma type.
We can extract the first part using `fst` or the second part using `snd`.
Given `x : Σ A B` there are three interpretations of `fst` and `snd`:
- Viewing `x` as a proof of existence
`fst x` provides the witness of existence and `snd` provides the proof
that the witness `fst x` has the desired property
- Viewing `x` as a recipe `fst` extracts the first component and
`snd` extracts the second component
- Viewing `x` as a point in the total space of a bundle
`fst x` is the point that `x` is over in the base space and `snd x`
is the point in the fiber that `x` represents.
In particular you can interpret `fst` as projection from the total space
to the base space, collapsing fibers.
For example to define a map that takes an even natural and divides it by two
we can do
```agda
div2 : Σ ℕ isEven → ℕ
div2 x = ?
```
- Load the file, go to the hole and case on `x`.
You might want to rename `fst₁` and `snd₁`.
```agda
div2 : Σ ℕ isEven → ℕ
div2 (fst₁ , snd₁) = {!!}
```
- Case on `fst₁` and tell agda what to give for `0 , _`,
i.e. what 'zero divided by two' ought to be.
```agda
div2 : Σ ℕ isEven → ℕ
div2 (zero , snd₁) = {!!}
div2 (suc fst₁ , snd₁) = {!!}
```
- Navigate to the second hole and case on `fst₁` again.
Notice that agda knows there is no term looking like `1 , _`
so it has skipped that case for us.
```agda
div2 : Σ ℕ isEven → ℕ
div2 (zero , snd₁) = 0
div2 (suc (suc fst₁) , snd₁) = {!!}
```
- `(n + 2) / 2` should just be `n/2 + 1`
so try writing in `suc` and refining the goal
- How do you write down `n/2`? Hint: we are in the 'inductive step'.
Try dividing some terms by `2`:
- Use `C-c C-n` and write `div2 (2 , tt)` for example.
- Try dividing `36` by `2`.
*Important Observation* :
the two proofs `2 , tt` and `36 , tt` of the statement
'there exists an even natural' are not 'the same' in any sense,
since if they were `div2 (2 , tt)` would be 'the same' `div2 (36/2 , tt)`,
and hence `1` would be 'the same' as `18`.
> Are they 'the same'? What is 'the same'?
which can also be viewed as the subset of even naturals,
since the fibers are either empty or singleton.
(It is a _subsingleton bundle_).
Making a term of this type has three interpretations:
- a natural `n : ℕ` together with a proof `hn : isEven n` that `n` is even.
- a recipe `n : ℕ` together with a recipe `hn : isEven n`.
- a point in the total space is a point `n : ℕ` downstairs
together with a point `hn : isEven n` in its fiber.
Now you can prove that there exists an even natural:
- Formulate the statement you need. Make sure you have it of the form
```agda
Name : Statement
Name = ?
```
- Load the file, go to the hole and refine the goal.
- If you formulated the statement right it should split into `{!!} , {!!}`
and you can check the types of terms the holes require.
- Fill the holes. There are many proofs you can do!
In general when `A : Type` is a type and `B : A → Type` is a
predicate/dependent construction/bundle over `A`,
we can write the sigma type `Σ A B` whose terms are pairs `a , b`
where `a : A` and `b : B a`.
In the special case when `B` is not dependent on `a : A`,
i.e. it looks like `λ a → C` for some `C : Type` then
`Σ A B` is just
- the proposition '`A` and `C`'
since giving a proof of this is the same as giving a proof
of `A` and a proof of `C`
- a recipe `a : A` together with a recipe `c : C`
- `B` is now a _trivial bundle_ since the fibers `B a` are
constant with respect to `a : A`.
In other words it is just a _product_ `Σ A B ≅ A × C`.
For this reason,
some refer to the sigma type as the _dependent product_,
but we will avoid this terminology.
```agda
_×_ : Type → Type → Type
A × C = Σ A (λ a → C)
```
Agda supports the notation `_×_` (without spaces)
which means from now on you can write `A × C` (with spaces).
There are two ways of using a term in a sigma type.
We can extract the first part using `fst` or the second part using `snd`.
Given `x : Σ A B` there are three interpretations of `fst` and `snd`:
- Viewing `x` as a proof of existence
`fst x` provides the witness of existence and `snd` provides the proof
that the witness `fst x` has the desired property
- Viewing `x` as a recipe `fst` extracts the first component and
`snd` extracts the second component
- Viewing `x` as a point in the total space of a bundle
`fst x` is the point that `x` is over in the base space and `snd x`
is the point in the fiber that `x` represents.
In particular you can interpret `fst` as projection from the total space
to the base space, collapsing fibers.
For example to define a map that takes an even natural and divides it by two
we can do
```agda
div2 : Σ ℕ isEven → ℕ
div2 x = ?
```
- Load the file, go to the hole and case on `x`.
You might want to rename `fst₁` and `snd₁`.
```agda
div2 : Σ ℕ isEven → ℕ
div2 (fst₁ , snd₁) = {!!}
```
- Case on `fst₁` and tell agda what to give for `0 , _`,
i.e. what 'zero divided by two' ought to be.
```agda
div2 : Σ ℕ isEven → ℕ
div2 (zero , snd₁) = {!!}
div2 (suc fst₁ , snd₁) = {!!}
```
- Navigate to the second hole and case on `fst₁` again.
Notice that agda knows there is no term looking like `1 , _`
so it has skipped that case for us.
```agda
div2 : Σ ℕ isEven → ℕ
div2 (zero , snd₁) = 0
div2 (suc (suc fst₁) , snd₁) = {!!}
```
- `(n + 2) / 2` should just be `n/2 + 1`
so try writing in `suc` and refining the goal
- How do you write down `n/2`? Hint: we are in the 'inductive step'.
Try dividing some terms by `2`:
- Use `C-c C-n` and write `div2 (2 , tt)` for example.
- Try dividing `36` by `2`.
*Important Observation* :
the two proofs `2 , tt` and `36 , tt` of the statement
'there exists an even natural' are not 'the same' in any sense,
since if they were `div2 (2 , tt)` would be 'the same' `div2 (36/2 , tt)`,
and hence `1` would be 'the same' as `18`.
> Are they 'the same'? What is 'the same'?
 In the categorical perspective, for each `n : ℕ`
`isEven n` is called the _fiber over `n`_.
In this particular example the fibers are either empty
or singleton.
In general given a type `A : Type`,
a _dependent type over `A`_ is a term of type `A → Type`.
You can check if `2` is even by asking agda to 'reduce' the term `isEven 2`:
do `C-c C-n` (`n` for normalize) and type in `isEven 2`.
(By the way you can write in numerals since we are now secretly
using `ℕ` from the cubical agda library.)
Now that we have expressed `isEven` we need to be able write down "existence".
In maths we might write
```
∃ x ∈ ℕ, isEven x
```
which in agda notation is
```
Σ ℕ isEven
```
This is called a _sigma type_, which has three interpretations:
- the proposition 'there exists an even natural'
- the construction
'keep a recipe `n` of naturals together with a recipe of `isEven n`'
- the total space of the bundle `isEven` over `ℕ`,
which is the space obtained by putting together all the fibers.
Pictorially, it looks like
In the categorical perspective, for each `n : ℕ`
`isEven n` is called the _fiber over `n`_.
In this particular example the fibers are either empty
or singleton.
In general given a type `A : Type`,
a _dependent type over `A`_ is a term of type `A → Type`.
You can check if `2` is even by asking agda to 'reduce' the term `isEven 2`:
do `C-c C-n` (`n` for normalize) and type in `isEven 2`.
(By the way you can write in numerals since we are now secretly
using `ℕ` from the cubical agda library.)
Now that we have expressed `isEven` we need to be able write down "existence".
In maths we might write
```
∃ x ∈ ℕ, isEven x
```
which in agda notation is
```
Σ ℕ isEven
```
This is called a _sigma type_, which has three interpretations:
- the proposition 'there exists an even natural'
- the construction
'keep a recipe `n` of naturals together with a recipe of `isEven n`'
- the total space of the bundle `isEven` over `ℕ`,
which is the space obtained by putting together all the fibers.
Pictorially, it looks like
 which can also be viewed as the subset of even naturals,
since the fibers are either empty or singleton.
(It is a _subsingleton bundle_).
Making a term of this type has three interpretations:
- a natural `n : ℕ` together with a proof `hn : isEven n` that `n` is even.
- a recipe `n : ℕ` together with a recipe `hn : isEven n`.
- a point in the total space is a point `n : ℕ` downstairs
together with a point `hn : isEven n` in its fiber.
Now you can prove that there exists an even natural:
- Formulate the statement you need. Make sure you have it of the form
```agda
Name : Statement
Name = ?
```
- Load the file, go to the hole and refine the goal.
- If you formulated the statement right it should split into `{!!} , {!!}`
and you can check the types of terms the holes require.
- Fill the holes. There are many proofs you can do!
In general when `A : Type` is a type and `B : A → Type` is a
predicate/dependent construction/bundle over `A`,
we can write the sigma type `Σ A B` whose terms are pairs `a , b`
where `a : A` and `b : B a`.
In the special case when `B` is not dependent on `a : A`,
i.e. it looks like `λ a → C` for some `C : Type` then
`Σ A B` is just
- the proposition '`A` and `C`'
since giving a proof of this is the same as giving a proof
of `A` and a proof of `C`
- a recipe `a : A` together with a recipe `c : C`
- `B` is now a _trivial bundle_ since the fibers `B a` are
constant with respect to `a : A`.
In other words it is just a _product_ `Σ A B ≅ A × C`.
For this reason,
some refer to the sigma type as the _dependent product_,
but we will avoid this terminology.
```agda
_×_ : Type → Type → Type
A × C = Σ A (λ a → C)
```
Agda supports the notation `_×_` (without spaces)
which means from now on you can write `A × C` (with spaces).
There are two ways of using a term in a sigma type.
We can extract the first part using `fst` or the second part using `snd`.
Given `x : Σ A B` there are three interpretations of `fst` and `snd`:
- Viewing `x` as a proof of existence
`fst x` provides the witness of existence and `snd` provides the proof
that the witness `fst x` has the desired property
- Viewing `x` as a recipe `fst` extracts the first component and
`snd` extracts the second component
- Viewing `x` as a point in the total space of a bundle
`fst x` is the point that `x` is over in the base space and `snd x`
is the point in the fiber that `x` represents.
In particular you can interpret `fst` as projection from the total space
to the base space, collapsing fibers.
For example to define a map that takes an even natural and divides it by two
we can do
```agda
div2 : Σ ℕ isEven → ℕ
div2 x = ?
```
- Load the file, go to the hole and case on `x`.
You might want to rename `fst₁` and `snd₁`.
```agda
div2 : Σ ℕ isEven → ℕ
div2 (fst₁ , snd₁) = {!!}
```
- Case on `fst₁` and tell agda what to give for `0 , _`,
i.e. what 'zero divided by two' ought to be.
```agda
div2 : Σ ℕ isEven → ℕ
div2 (zero , snd₁) = {!!}
div2 (suc fst₁ , snd₁) = {!!}
```
- Navigate to the second hole and case on `fst₁` again.
Notice that agda knows there is no term looking like `1 , _`
so it has skipped that case for us.
```agda
div2 : Σ ℕ isEven → ℕ
div2 (zero , snd₁) = 0
div2 (suc (suc fst₁) , snd₁) = {!!}
```
- `(n + 2) / 2` should just be `n/2 + 1`
so try writing in `suc` and refining the goal
- How do you write down `n/2`? Hint: we are in the 'inductive step'.
Try dividing some terms by `2`:
- Use `C-c C-n` and write `div2 (2 , tt)` for example.
- Try dividing `36` by `2`.
*Important Observation* :
the two proofs `2 , tt` and `36 , tt` of the statement
'there exists an even natural' are not 'the same' in any sense,
since if they were `div2 (2 , tt)` would be 'the same' `div2 (36/2 , tt)`,
and hence `1` would be 'the same' as `18`.
> Are they 'the same'? What is 'the same'?
which can also be viewed as the subset of even naturals,
since the fibers are either empty or singleton.
(It is a _subsingleton bundle_).
Making a term of this type has three interpretations:
- a natural `n : ℕ` together with a proof `hn : isEven n` that `n` is even.
- a recipe `n : ℕ` together with a recipe `hn : isEven n`.
- a point in the total space is a point `n : ℕ` downstairs
together with a point `hn : isEven n` in its fiber.
Now you can prove that there exists an even natural:
- Formulate the statement you need. Make sure you have it of the form
```agda
Name : Statement
Name = ?
```
- Load the file, go to the hole and refine the goal.
- If you formulated the statement right it should split into `{!!} , {!!}`
and you can check the types of terms the holes require.
- Fill the holes. There are many proofs you can do!
In general when `A : Type` is a type and `B : A → Type` is a
predicate/dependent construction/bundle over `A`,
we can write the sigma type `Σ A B` whose terms are pairs `a , b`
where `a : A` and `b : B a`.
In the special case when `B` is not dependent on `a : A`,
i.e. it looks like `λ a → C` for some `C : Type` then
`Σ A B` is just
- the proposition '`A` and `C`'
since giving a proof of this is the same as giving a proof
of `A` and a proof of `C`
- a recipe `a : A` together with a recipe `c : C`
- `B` is now a _trivial bundle_ since the fibers `B a` are
constant with respect to `a : A`.
In other words it is just a _product_ `Σ A B ≅ A × C`.
For this reason,
some refer to the sigma type as the _dependent product_,
but we will avoid this terminology.
```agda
_×_ : Type → Type → Type
A × C = Σ A (λ a → C)
```
Agda supports the notation `_×_` (without spaces)
which means from now on you can write `A × C` (with spaces).
There are two ways of using a term in a sigma type.
We can extract the first part using `fst` or the second part using `snd`.
Given `x : Σ A B` there are three interpretations of `fst` and `snd`:
- Viewing `x` as a proof of existence
`fst x` provides the witness of existence and `snd` provides the proof
that the witness `fst x` has the desired property
- Viewing `x` as a recipe `fst` extracts the first component and
`snd` extracts the second component
- Viewing `x` as a point in the total space of a bundle
`fst x` is the point that `x` is over in the base space and `snd x`
is the point in the fiber that `x` represents.
In particular you can interpret `fst` as projection from the total space
to the base space, collapsing fibers.
For example to define a map that takes an even natural and divides it by two
we can do
```agda
div2 : Σ ℕ isEven → ℕ
div2 x = ?
```
- Load the file, go to the hole and case on `x`.
You might want to rename `fst₁` and `snd₁`.
```agda
div2 : Σ ℕ isEven → ℕ
div2 (fst₁ , snd₁) = {!!}
```
- Case on `fst₁` and tell agda what to give for `0 , _`,
i.e. what 'zero divided by two' ought to be.
```agda
div2 : Σ ℕ isEven → ℕ
div2 (zero , snd₁) = {!!}
div2 (suc fst₁ , snd₁) = {!!}
```
- Navigate to the second hole and case on `fst₁` again.
Notice that agda knows there is no term looking like `1 , _`
so it has skipped that case for us.
```agda
div2 : Σ ℕ isEven → ℕ
div2 (zero , snd₁) = 0
div2 (suc (suc fst₁) , snd₁) = {!!}
```
- `(n + 2) / 2` should just be `n/2 + 1`
so try writing in `suc` and refining the goal
- How do you write down `n/2`? Hint: we are in the 'inductive step'.
Try dividing some terms by `2`:
- Use `C-c C-n` and write `div2 (2 , tt)` for example.
- Try dividing `36` by `2`.
*Important Observation* :
the two proofs `2 , tt` and `36 , tt` of the statement
'there exists an even natural' are not 'the same' in any sense,
since if they were `div2 (2 , tt)` would be 'the same' `div2 (36/2 , tt)`,
and hence `1` would be 'the same' as `18`.
> Are they 'the same'? What is 'the same'?